Enoncé
Soit la suite
)
définie par récurrence par :
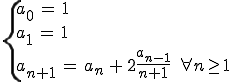
1. Déterminer le rayon de convergence de la série entière :
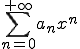
.
2. Déterminer la somme de cette série (on pourra s'aider d'une équation différentielle).
Méthode de résolution
Solution
Pour simplifier les calculs par la suite et éviter les problèmes d'indice, on peut poser :
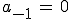
.
1.
On doit trouver
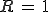
.
L'encadrement de
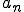
nous donne d'une part que la série de terme général
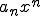
a un rayon de convergence inférieur ou égal à celui de la série de terme général
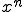
(i.e. 1). D'autre part que ce rayon est supérieur ou égal à celui de la série de terme général
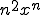
(égal lui aussi à 1 par le critère de d'Alembert).
Attention ! Ne pas majorer trop brutalement pendant le raisonnement par récurrence, mais plutôt raisonner par équivalences.
2.
On obtient l'équation différentielle suivante :
\,-\, \frac{1+2x}{1-x}f(x)\,=\,0)
On doit calculer la primitive de
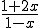
. On décompose cette fraction en éléments simples de la forme :
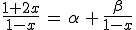
.
On trouve
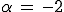
et
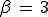
, ce qui permet de calculer la primitive, et de terminer la résolution de l'équation.
Finalement, on trouve :
 \,=\, \frac {\exp(-2x)}{(1-x)^{3}})
, ce qui est la somme demandée.
Cet exercice peut s'avérer délicat à certains endroits, et ce qui est exposé ici est la démarche générale, sans entrer dans les détails. Si vous avez un problème à un endroit de la résolution, vous pouvez poser vos questions sur le
Bar à Nougat.
en l'exprimant à l'aide d'une série numérique.