Calculer l'intégrale suivante :
}\, \mathrm d \theta)
Eléments de réponse
- Commencez par vérifier que cette intégrale est bien intégrable.
- Ensuite, faites un changement de variables.
- Il ne reste plus qu'à décomposer en éléments simples... Et c'est là que ça se complique. Bon courage ;)
Réponse
- Intégrabilité : Le seul problème est en
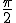 , donc posons
, donc posons 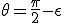 où
où  tend vers 0.
tend vers 0.
Alors  = \frac{1}{\tan(\epsilon)})
Donc en effectuant un DL (ordre 1) de }) , on voit que cette fonction converge. Donc elle est intégrable sur
, on voit que cette fonction converge. Donc elle est intégrable sur 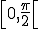
- Changement de variable avec
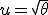 donc
donc 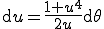 . On a alors :
. On a alors :
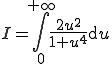
- Et là deux solutions s'offrent à nous, soit on fait la décomposition en éléments simples avec pleins de calculs, soit on décompose en réels, ce qui allège un peu les calculs. Je détaille ci-dessous le début de la première méthode, puis rapidement la deuxième.
[liste_s]Cherchons les racines du dénominateur :
![1+u^4 = 0 ,, Longleftrightarrow ,, u^4=-1=1 , e^{i pi} ,, Longleftrightarrow ,, u=sqrt[4]{1} , e^{i frac{pi}{4}} = sqrt[4]{1} omega 1+u^4 = 0 \,\, \Longleftrightarrow \,\, u^4=-1=1 \, e^{i \pi} \,\, \Longleftrightarrow \,\, u=\sqrt[4]{1} \, e^{i \frac{\pi}{4}} = \sqrt[4]{1} \omega](cgi-bin/latex.cgi?1+u^4 = 0 \,\, \Longleftrightarrow \,\, u^4=-1=1 \, e^{i \pi} \,\, \Longleftrightarrow \,\, u=\sqrt[4]{1} \, e^{i \frac{\pi}{4}} = \sqrt[4]{1} \omega)
Donc  = (1+\omega)(1-\omega)(1+i \omega)(1-i \omega))
Il ne reste plus qu'à trouver les quatre constantes de la décomposition en éléments simples.[/liste_s]
[liste_s]On décompose en réel :
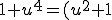^2 + (\sqrt{2}u)^2 = (u^2 - \sqrt{2}u +1)(u^2 + \sqrt{2}u +1))
On doit donc trouver quatre constantes :
(u^2 + \sqrt{2}u +1)} = \frac{Au+B}{(u^2 + \sqrt{2}u +1)} + \frac{Cu+D}{(u^2 - \sqrt{2}u +1)})
On peut remarquer que 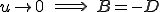 et
et 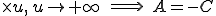
On remplace, on développe et on trouve : 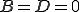 et
et 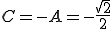 [/liste_s]
[/liste_s]
- Reste à calculer I... On pose :
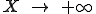 . On a :
. On a : ' = (2u \pm \sqrt{2})) . On a alors :
. On a alors :
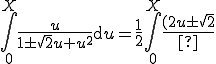 \mp \sqrt{2}}{1 \pm \sqrt{2}u+u^2} \mathrm{d}u = \frac{1}{2} \int_0^{X} \frac{2u \pm \sqrt{2}}{1 \pm \sqrt{2}u+u^2} \mathrm{d}u \, \mp \, \frac{\sqrt2}{2} \int_0^{X} \frac{\mathrm{d}u}{1 \pm \sqrt{2}u+u^2})
Sachant que :
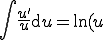)
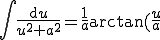)
En terminant les calculs et en prenant les deux parties de l'intégrales, on obtient : 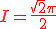
Cet exercice peut s'avérer délicat à certains endroits, et ce qui est exposé ici est la démarche générale, sans entrer dans les détails. Si vous avez un problème à un endroit de la résolution, vous pouvez poser vos questions sur le
Bar à Nougat.
}\, \mathrm d \theta)