Vous êtes ici : Accueil > Concours > Grandes écoles >PSI - Exercice d'oral [Géométrie, Quadrique]

Concours -Grandes écoles

PSI - Exercice d'oral [Géométrie, Quadrique]

  • Auteur :Bnmaster
  • Créé le :18/06/2008
  • Modifié le :22/06/2012
Donner la nature de xy + yz + zx = 1 (1)

Réponse
On cherche la nature d'une quadrique. Posons :
A = \begin{pmatrix} 0

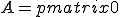
(1) est donc équivalente à : ^tXAX=1
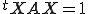
Or A \in S_n(\mathbb{R}), donc d'après le théorème spectral : \exists P \in O_n(\mathbb{R}) \,\, \exists D \in D_n(\mathbb{R}) \,\, A=PDP^{-1}

On pourrait calculer le polynôme caractéristique de A (à la main) assez rapidement, mais voici une petite astuce pas mal, on remarque :
B = \begin{pmatrix} 1
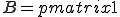
Le polynôme annulateur de B se calcule de tête en raisonnant sur le rang et la trace de B, on a \chi_B(X)=-X^2(X-3). Par conséquent, on a :
D = \begin{pmatrix} 1

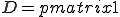
Donc en posant Y=\begin{pmatrix} x' \\ y' \\ z' \end{pmatrix}=P^{-1}X
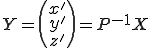
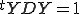
(1) équivaut à ^tYDY=1 dont équivaut à \frac{y'}{\sqrt{2}}^2 + \frac{z'}{\sqrt{2}}^2 - {x'}^2 = -1

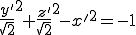
De par la forme de cette dernière équation, on peut dire que cette quadrique est un hyperboloïde à 2 nappes.