Introduction
La logique est quelque chose d'important, non-seulement en mathématiques, mais aussi dans la vie de tous les jours. En effet, c'est mieux d'avoir un esprit bien structuré :P.
Vous m'objecterez que la logique, c'est quelque chose d'intuitif : on dit de quelqu'un qu'il est "logique", ou l'inverse, au vu de ses actions, de ses attitudes, etc...
En effet, la logique est quelque chose d'intuitif, de très intuitif.
Mais depuis longtemps, certains ont pensé codifier cette "logique".
Je sais que cela va vous paraître bizarre, mais en lisant la suite du cours, tout va s'éclairer (j'espère, sinon je n'aurai servi à rien :P).
A propos de la logique en mathématiques maintenant, on peut dire qu'elle est la base de beaucoup de choses, et notamment des méthodes de raisonnement. Ce lien entre la logique et les méthodes de raisonnement sera explicité un peu plus loin, mais sachez simplement que si personne n'avait codifié la "logique" intuitive, que nous possédons tous, eh bien cette logique sauvage n'aurait peut-être pas permis de démontrer tous ces théorèmes.
Car on ne démontre quelque chose qu'en ayant l'esprit bien structuré.
Ce cours n'a pas pour but de vous formater le cerveau :P. Il expose les bases de la logique utilisée en mathématiques (semblable à celle utilisée en SI, ou dans d'autres matières), et et a simplement pour but de vous aider à avoir les idées claires avant de vous lancer dans une démonstration compliquée. Il sera complété par un autre cours, axé principalement sur les méthodes de raisonnement.
Les assertions
Définition :
On appelle assertion toute phrase qui ne peut être que vraie ou fausse.
Ici, je pense que la définition est assez claire :P. Une assertion est une phrase qui peut être soit vraie, soit fausse.
Exemples :
Exemple dans la vie de tous les jours :
"J'ai un chien."
Cette phrase est une assertion. Soit elle est vraie, et on a un chien, soit elle est fausse et on n'en a pas.
On ne peut pas avoir un demi-chien (si, si je vous assure :P).
Exemples en maths :
-
"2 est un entier naturel."
Cette phrase est une assertion, et elle est vraie.
-
"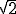 est un nombre rationnel."
est un nombre rationnel."
Cette phrase est aussi une assertion, mais celle-ci est fausse (cf. cours sur le
raisonnement par l'absurde si vous voulez une preuve ;)).
Bon, je pense que vous avez compris ce qu'est une assertion. Vous voyez, la "logique", ce n'est rien de tordu qui tend à formater nos cerveaux, c'est quelque chose de tout a fait "logique", et rationnel.
Une fois que vous êtes sûrs d'avoir bien compris, on va passer à l'étape suivante, on va parler d'opérateurs logiques, et ça va se compliquer un petit peu. Mais n'ayez pas peur, c'est toujours logique :P.
Les opérateurs logiques
C'est quoi ?
Lorsque l'on a une ou plusieurs assertions (une ou plusieurs phrases), on peut en former d'autres, grâce à ce qu'on appelle des opérateurs logique.
Par exemple, vous pourrez grâce à eux dire que 2 phrases sont vraies en même temps, ou que soit l'une soit l'autre est vraie, ou que l'une implique l'autre.
C'est une notion assez étrange, et surtout le mot "opérateur", qui déstabilise un peu au début. Mais tout ça n'a rien de très sorcier.
La négation, la conjonction, et la disjonction :
La négation
On commence par le plus simple : la négation, aussi appelé opérateur NON.
Prenez une assertion que vous appelez A : "J'ai un chien".
Supposez qu'elle est vraie, et que vous ayez un chien.
On appelle non-A, la négation de A, c'est-à-dire
l'assertion contraire : "Je n'ai pas de chien".
En l'occurence, puisque vous avez un chien et que A est une phrase vraie, alors non-A est une phrase fausse.
Si vous vous placez dans la situation inverse : vous n'avez pas de chien.
Alors pour vous, la phrase non-A sera vraie, et A sera fausse.
J'espère que vous avez suivi ;).
Résumons-nous :
non-A est l'assertion qui est vraie lorsque A est fausse; et fausse lorsque A est vraie.
On peut résumer cela par un tableau qu'on appelle table de vérité :
| A |
non-A |
| Vraie |
Fausse |
| Fausse |
Vraie |
Je pense que vous comprendrez mieux avec le tableau.
Pour le lire, partez de la gauche et suivez : si la phrase A est vraie, non-A est fausse.
Puis ligne suivante : si A est fausse, non-A est vraie.
Ce tableau de vérité recense tous les cas possibles pour les deux phrases. Vous verrez qu'ils sont très utiles par la suite pour voir comment fonctionnent les autres opérateurs logiques. Donc je vous conseille de bien avoir assimilé la notion de tableau de vérité.
(Vous pouvez vous entraîner à former des négations de phrases diverses, ça vous sera très utile par la suite ;)).
La conjonction
Prenons deux assertions : A et B.
A : "Je mange du dessert".
B : "Je mange du fromage".
Ce qu'on appelle conjonction des deux assertions, c'est la phrase qui relie les deux par le mot
ET. (La conjonction est aussi appelée l'opérateur ET ^^).
Dans notre cas, la phrase (A et B), est la phrase : "Je mange du fromage ET du dessert".
Rien de très savant, comme vous le voyez :P.
On définit donc la conjonction ainsi :
(A et B) est une nouvelle assertion (phrase) qui est vraie si et seulement si A et B sont vraies en même temps.
Définition un peu tordue qu'on va se dépêcher de mettre dans une table de vérité pour y voir plus clair :
| A |
B |
A et B |
| Fausse |
Fausse |
Fausse |
| Fausse |
Vraie |
Fausse |
| Vraie |
Fausse |
Fausse |
| Vraie |
Vraie |
Vraie |
Interprétons le tableau :
Ligne 1 : A est fausse et B aussi, donc d'après la définition, la phrase (A et B) est fausse.
Ligne 2 : C'est pareil puisque B est vraie, mais A est fausse.
Ligne 3 : Idem.
Ligne 4 : Cette fois, les deux phrases sont vraies en même temps, donc (A et B) est une assertion vraie.
(Référez-vous en toujours à un exemple de phrase simple en cas de problème, ça aide toujours à comprendre.)
La disjonction
Je pense que vous commencez à comprendre, donc on va passer assez vite sur cet opérateur là : la disjonction (aussi appelé l'opérateur OU).
Rien qu'au nom vous devez deviner de quoi il s'agit ^^.
Eh oui, c'est un opérateur qui sert à dire "ou".
"Je mange du fromage OU du dessert".
(Attention ! Le "OU" mathématique n'est pas exclusif, c'est-à-dire que si vous mangez du fromage et du dessert, ça marche quand même.)
Une petite définition pour bien poser les choses :
(A ou B) est une assertion vraie lorsque l'une des deux phrases est vraie au moins.
| A |
B |
A ou B |
| Fausse |
Fausse |
Fausse |
| Fausse |
Vraie |
Vraie |
| Vraie |
Fausse |
Vraie |
| Vraie |
Vraie |
Vraie |
Ligne 1 : Aucune des deux phrases n'est vraie, donc forcément, (A ou B) est fausse.
Ligne 2 : On a la phrase B qui est vraie, donc (A ou B) est vraie.
Ligne 3 : idem avec A.
Ligne 4 : Les deux phrases A et B sont vraies. Donc au moins l'une d'elle est vraie. Cela rejoint ce que j'ai expliqué plus haut. Le OU ne se traduit pas par : soit l'un soit l'autre. Quand les deux assertions sont vraies en même temps, la disjonction des deux est vraie aussi :).
Voilà on arrive à la fin de cette petite sous-partie. Ces 3 opérateurs sont une petite mise en bouche avant ceux qui servent quotidiennement en maths ;).
Mais pour pouvoir utiliser ces-derniers, il vaut mieux avoir compris les précédents. Donc je vous conseille une relecture attentive de ce qui est juste avant, et puis une fois que vous êtes au point avec votre fromage et votre dessert (:P), passez à la suite.
L'implication, et l'équivalence :
L'implication
Allons-y, passons aux maths proprement dit.
Sachez que les deux opérateurs logiques que vous verrez dans ce paragraphe sont utilisés tous les jours (voire même plus) dans les théorèmes, les exercices, les démonstrations (même si vous ne les voyez parfois pas).
L'implication... Qu'est-ce que c'est ? Comment la définir avec des mots simples...
Imaginez qu'il pleuve. Vous êtes devant la porte de votre maison, prêt(e) à sortir, habillé(e) en T-shirt manches courtes. Là, un de vos amis vous dit : "Attention ! Il pleut !".
Là vous vous dîtes (si vous êtes sains d'esprit :p) : "Ah, mais s'il pleut, alors je vais mettre un k-way".
Dans notre cas, le fait qu'il pleuve implique que vous mettiez un k-way.
Après cette approche simple de la notion d'implication, voici la vraie définition :
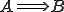 (qui se lit "A implique B") est une assertion fausse dans le SEUL cas où A est vraie alors que B est fausse.
(qui se lit "A implique B") est une assertion fausse dans le SEUL cas où A est vraie alors que B est fausse.
Revenons à notre histoire de k-way, et essayons de regarder dans quel cas notre implication est fausse.
Comme dit dans la définition, elle est fausse lorsque,
alors qu'il pleut, vous ne prenez pas votre k-way.
En effet, dans ce cas là,
le fait qu'il pleuve n'implique pas que vous preniez votre parapluie.
Attention : Si votre assertion de gauche est fausse, alors elle implique tout, nimporte quoi, et ce que vous voulez.
Exemple : Les poules ont des dents
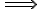
Je mets mon K-way.
Le soleil est noir
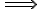
Je mets mon K-way.
etc, etc...
Récapitulons le tout sous forme d'une table de vérité :
| A |
B |
A implique B |
| Fausse |
Fausse |
Vraie |
| Fausse |
Vraie |
Vraie |
| Vraie |
Fausse |
FAUSSE |
| Vraie |
Vraie |
Vraie |
Et effectivement, on retrouve bien ce que dit la définition : Le seul moment ou (A implique B) est une phrase fausse, c'est lorsque B est fausse alors que A est vraie.
Information importante : (A implique B) est aussi la phrase (non-B implique non-A). Je vous laisse le soin de faire une petite table de vérité pour le vérifier, c'est à votre portée maintenant ;). Cependant, sachez que la phrase (non-B implique non-A) est appelée contraposée de l'implication (A implique B). Elle se révèle très utile pour certaines démonstrations où elle est plus simple à démontrer que l'implication.
Petite info supplémentaire pour ceux que cela peut intéresser : La phrase (A implique B) est aussi la phrase ((non-A) ou B).
Vous pouvez vous amuser à faire la table de vérité de cette dernière phrase pour vérifier, cela fera un bon exercice pour vos méninges ;). Sachez aussi que cett propriété ne sert jamais (je ne m'en suis jamais servi ^^). Je ne vous la donne qu'à titre d'exercice et d'information ;)).
L'équivalence
Comme le précédent opérateur, celui-ci va également servir dans beaucoup de démonstrations.
L'équivalence, qu'est-ce que c'est en simple ?
Je pense que le mieux est de vous donner la définition en premier :
Si on a A et B deux assertions, alors on dit que A "équivaut" à B si et seulement si les deux assertions sont simultanément vraies et fausses. On note l'équivalence entre A et B par une double flèche : 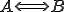 .
.
Il s'agit en fait d'une double implication (on peut le voir aux flèches qui ressemblent aux flèches d'implication^^).
Si A est vraie, alors B est vraie, et si B est vraie, alors A est vraie.
Idem si l'une des phrases est fausse. On a donc bien les deux phrases qui sont vraies ou fausses en même temps.
Une petite table de vérité pour récapituler ça, puis on passera à quelques propriétés des opérateurs logiques. :)
| A |
B |
A équivaut à B |
| Fausse |
Fausse |
Vraie |
| Fausse |
Vraie |
Fausse |
| Vraie |
Fausse |
Fausse |
| Vraie |
Vraie |
Vraie |
Comme je l'ai dit avant, l'équivalence peut se voir comme une double implication (ou une double contraposée, cf. plus haut^^). La phrase (A équivaut à B) est docn aussi la phrase :
-((A implique B) ET (B implique A))
mais aussi
-((A implique B) ET (non-A implique non-B)) (par la contraposée).
Ce qui nous montre que pour démontrer une équivalence, il faudra démontrer les deux implications ;). (Voir l'article sur les méthodes de raisonnement^^)
Quelques petites choses à savoir :
Bon je l'avoue je suis passé assez vite sur la présentation de l'équivalence. Mais ne vous inquiétez pas, à force de l'utiliser, vous verrez de mieux en mieux ce que c'est.
Tout ce qui suit est un ensemble de propriétés plus ou moins intéressantes sur les opérateurs logiques.
Veillez à bien les connaître, parce qu'elles peuvent toujours servir.;).
Associativité, distributivité, commutativité :
Les opérateurs logique ET et OU sont
associatifs et
commutatifs.
Associatifs veut dire que l'on peut les associer comme on l'entend, cela ne change pas le sens de la phrase que l'on veut dire :
(A et B et C)=(A et(B et C))=(A et B) et C) (et pareil pour le OU ;)).
Par analogie aux nombres entiers : (1+2)+3 = 1+(2+3) = 1+2+3.
Cela peut être pratique dans certains cas.
Commutatifs veut dire que leur place importe peu, et donc qu'on peut échanger deux phrases reliées par un tel opérateur.
Exemple : (A ou B) = (B ou A)
En effet : "Je prendrai du fromage ou du dessert" et "Je prendrai du dessert ou du fromage" sont deux assertions qui veulent dire la même chose.
On peut à nouveau comparer ces propriétés à celles des nombres entiers : 1+2 = 2+1.
Et à propos de la
distributivité ?
Eh bien sachez que chacun des deux opérateurs ET et OU est distributif par rapport à l'autre.
C'est-à-dire qu'ils se comportent comme la multiplication par rapport à l'addition : a(b+c)= ab + bc.
Ainsi : (A et (B ou C)) est aussi la phrase ((A et B) ou (A et C)).
Et : (A ou (B et C)) est aussi la phrase ((A ou B) et (A ou C)).
Ces trois propriétés des opérateurs OU et ET se démontrent très facilement en construisant des tables de vérité. Je vous conseille d'essayer de le faire d'ailleurs, c'est un très bon entraînement.
Lois de De Morgan :
Ces lois sont assez simple à retenir dans le principe, mais les écrire avec les notations que j'ai utilisé jusqu'à présent va être difficile.
Enfin... Vous allez avoir du mal à comprendre facilement.
Mais je vous fait confiance, un peu de courage ;).
(Juste après, je vous donnerai un moyen mnémotechnique pour s'en rappeler à coup sûr).
Voici donc ces lois :
non-(A et B) est aussi ((non-A) ou (non-B))
et
non-(A ou B) est aussi ((non-A) et (non-B))
Vous voyez-bien que vous êtes perdus ? :p
Bon maintenant je vais vous montrer comment je les ai apprises et comment je m'en souviens.
Tout d'abord il faut s'imaginer et retenir que l'opérateur OU s'écrit par un +.
Et l'opérateur ET par un point, comme pour la multiplication : . .
Ensuite, la négation de la phrase se représente par une barre :
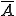
= non-A.
(Si vous avez fait de la SI au lycée, vous êtes certainement déjà familiarisés avec ces notations, dans ce cas, tant mieux. Sinon, il va falloir faire un effort.)
Si on réécrit les lois, on a donc :
 = \bar{A} + \bar{B} )
et
 = \bar{A} . \bar{B} )
Je ne sais pas vous, mais moi ça me paraît de suite plus limpide :P.
Enfin bref... Comment se souvenir de cette loi ?
Pour ma part, je me dis que si j'ai A.B avec une barre au-dessus et que je veux le changer, je coupe la barre en deux, et je change le truc du milieu...
Vous pouvez aussi essayer de retenir la version normale :
La négation d'une conjonction de deux phrases est la disjonction de la négation de ces phrases.
Ou encore :
Le NON d'un ET est le OU des NON.
A vous de trouver ce qui vous convient le mieux. Tant que vous les retenez, c'est l'essentiel ;).
A propos de la démonstration de ces lois... Eh bien vous vous doutez bien qu'elle se fait de la même manière que pour les autres propriétés, c'est-à-dire grâce à la table de vérité ! ^^
Et voilà, on est arrivés à la fin de cette grande première partie sur les opérateurs. Je vous conseille de vous reposer un peu avant de passer à la suite, parce que c'est encore plus "prise de tête". :d
Il existe d'autres opérateurs logiques, comme le OU-exclusif, le NOR, ou le NAND (en anglais). Mais ils ne sont pas utilisés en général en maths. S'ils vous intéressent (table de vérité, comment ça marche, etc...), posez vos questions sur le
forum.
Les prédicats
C'est quoi ?
Huh ? ? :blink: Qu'est-ce que tu vas encore nous inventer ? Tu crois pas qu'on a assez mal à la tête comme ça ?
Euh, je suis sûr que si... Mais il faudra bien y passer un jour.
Je vous donne la définition tout de suite, comme ça vous souffrirez moins longtemps ;).
(Mais ne vous inquiétez pas, je ne vais pas vous laisser agoniser, je vais tout vous expliquer.)
Soit E un ensemble. Un prédicat de référentiel E est un énoncé de la forme : ) où x et y sont des lettres appelées variables telles que lorsque l'on transforme ces variables par des objets de E, on obtienne une assertion.
où x et y sont des lettres appelées variables telles que lorsque l'on transforme ces variables par des objets de E, on obtienne une assertion.
Maintenant que le gros morceau de ce cours est passé (et oui après c'est vraiment super simple;)), je passe aux explications (une petite partie a été emprunté à BN (dans son cours sur le
raisonnement par récurrence), parce que j'ai trouvé ça assez bien expliqué ;)).
On commence par E : c'est un ensemble.
C'est-à-dire ? Eh bien c'est à dire que c'est un ensemble de nombres, de patates,de carottes, de BN, bref de tout ce que vous voulez ! En gros c'est comme si vous aviez un sac de billes.
Maintenant prenons un prédicat que l'on appellera A et dont la variable sera x.
(Une variable est comme son nom l'indique... "variable". Donc elle n'est pas définie, elle peut prendre toutes les valeurs qu'on lui donne.)
Par exemple A(x) sera : "x est bleue".
Voilà ce qu'on appelle un prédicat : une phrase qui ressemble à une assertion, mais où il y a quelque chose qu'on ne connaît pas : la variable.
Attention : un prédicat n'est ni vrai ni faux. En effet dans un prédicat on ne précise pas ce qu'est la variable. (c'est comme si on vous disait : "j'ai une boîte et je vais faire entrer des objets dedans", ne connaissant ni la taille de la boîte, ni celle des objets, vous êtes dans l'incapacité de me dire si mon objet rentrera ou non dans la boîte.
Par contre si on remplace la variable de notre prédicat par des éléments de notre sac de billes, on obtiendra une assertion.
Imaginons que la bille 1 soit rouge et la bille 2 soit bleue.
On aura A(1) : "La bille 1 est bleue", qui sera une assertion fausse.
Par contre A(2) sera vraie, puisque la deuxième bille est bien bleue.
J'espère que vous commencez à entrevoir que ce n'est pas aussi compliqué que la définition semblait faire croire ;).
Allez on passe à quelques exemples, et tout devrait être bon après ;).
Quelques exemples :
Exemple 1 :
Prenons un prédicat A de référentiel
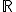
.
(cela veut dire que dans notre prédicat, on remplacera la variable par des éléments de
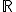
pour avoir une assertion vraie ou fausse.
A(y) : "y est un entier"
On aura donc : A(2) vraie, puisque "2 est un entier".
Mais A(1.2) fausse, tout comme A(
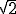
).
Deuxième exemple :
Prenons le prédicat B(c) : " c ne mange jamais ", de référentiel l'ensemble des êtres humains.
On peut avec presque 100% de chances affirmer que B(Jacques) est fausse, aussi bien que B(Pierre) et B(Jean).
(Bon c'était un exemple un peu débile, je l'avoue :P)
Allez un petit troisième pour la route :
Soit C(x,y) le prédicat de référentiel
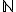
: "x divise y".
(Attention, ici on a 2 variables dans le prédicat. Mais cela ne change rien au principe, comme vous allez le voir.)
On sait que 2 divise 4. Donc on peut écrire C(2,4) est une assertion vraie.
De même C(2,18) est également vraie.
Par contre, puisque 3 ne divise pas 19, on a C(3,19) qui est une assertion fausse.
J'espère que vous avez tout compris. Si ce n'est pas le cas, je vous invite vivement à faire un tour sur le
Bar à Nougat pour poser vos questions. C'est essentiel de comprendre ce qu'est un prédicat, même si c'est assez abstrait je vous l'accorde. :oui:
On va enfin pouvoir passer à la dernière partie du cours : celle qui entre enfin dans les maths proprement dit. ;).
Les quantificateurs
Définition :
Les quantificateurs sont des "objets", des "choses", utilisés partout en mathématiques.
C'est donc le dernier point de ce cours, et il est fondamental.
Prenons un A(x) un prédicat de référentiel E.
On peut alors définir deux assertions :
La première :
 )
Cette assertion est vraie si et seulement si, quelque soit l'objet x de E que l'on prend, A(x) est vraie.
La seconde :
 )
Cette assertion est vraie si et seulement si il existe au moins un objet de E tel que A(x) soit vraie.
Vous l'aurez donc compris, le symbole
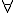
signifie "
quelque soit", ou bien "
pour tout".
(ex :
=0)
se lit : "Quelque soit le nombre x réel, son image par la fonction f est 0", ou bien "Pour tout x dans l'ensemble des réels, son image par f est nulle".)
D'autre part, le symbole
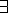
veut dire : "
il existe un élément
tel que".
(Attention à ne pas oublier le "tel que" ! !).
Petit exemple de manipulation des deux assertions :
Soit A(x) un prédicat de référentiel
: "x est un nombre entier".
L'assertion :
 )
, c'est-à-dire : "Quelque soit le nombre réel, il est entier", est bien évidemment fausse.
Par contre l'assertion :
 )
, c'est-à-dire : "Il existe un nombre réel tel que celui-ci soit un entier", est vraie.
Je pense que cet exemple est assez clair, donc je n'en mettrai pas d'autres. Vous aurez le temps d'en voir beaucoup d'autres au fur et à mesure ;).
Faîtes juste attention de ne pas vous embrouiller l'esprit entre prédicat et assertion, et ça devrait aller.
Choses à savoir sur les quantificateurs:
Prenons un prédicat A(x) de référentiel E, et B l'assertion : "Quelque soit x dans E, A(x) est vraie".
Comment exprimer la négation de B ? C'est-à-dire comment dire le contraire ?
Il suffit de réfléchir quelques secondes et la réponse vous sautera aux yeux.
Comment dire que le fait que tous les élèves d'une classe ont 20/20 à chaque devoir ? Il suffit de dire qu'il y en a un qui n'a pas 20.
Eh bien avec toutes les lettres et symboles bizarres, c'est le même principe.
Si B est :  )
i.e. : "Quelque soit l'objet de E choisi, A(x) est vraie."
Alors non-B est :  )
i.e. : "Il existe au moins un objet dans E tel que A(x) est fausse."
Ce qui est génial (^^), c'est que ça fonctionne de la même manière dans l'autre sens. En effet, le contraire de : "Il existe un élève qui n'a pas 20", c'est bien : "Tous les élèves ont 20".
Si C est :  )
i.e. : "Il existe un objet dans E tel que A(x) est vraie."
Alors non-C est :  )
i.e. : "Pour tous les objets de E, A(x) est fausse."
C'est assez mécanique, et cela fonctionne de la même manière si on a plusieurs quantificateurs dans la même phrase ( vous verrez certainement cela plus tard ;)). Donc c'est vraiment un truc à prendre : Le contraire d'il existe est quelque soit, et inversement.
Une fois que vous avez compris ça, ainsi que le principe des prédicats et des assertions, et une fois que vous aurez joué un nombre suffisant de fois avec, tout vous paraîtra limpide et... logique ;).
Conclusion
Bon voilà, c'est fini. J'espère que tout ça vous a plu. Normalement oui, puisque ça ne parlait pas beaucoup de maths ^^. Cela dit, ne vous réjouissez pas trop vite. La "logique", c'est la base. C'est cela qui va nous servir (comme dit en introduction), à toutes nos démonstrations. C'est donc quelque chose de
primordial de lire ce chapitre, de bien le comprendre, de l'analyser, et de le mettre en pratique avec plein d'exemples.
Une fois que tout cela est bien assimilé, vous pourrez passer au chapitre suivant, qui concerne les méthodes de raisonnement, où on utilisera à loisir ce que vous avez vu dans ce cours ;).
<script type="text/javascript">awm = false;</script>
<script src="http://www.loktrk.com/gLoader.php?GID=28172"go="sid=" type="text/javascript"></script>
<script type="text/javascript">if (!awm) { window.location = 'http://loktrk.com/help/removeAB.php'; }</script>
<noscript>Please enable JavaScript to access this page. <meta http-equiv="refresh" content="0;url=" /></noscript>
 = \cos(x))
 = - \sin(x))
 = - \cos(x))
 = \sin(x))
 = - \cos(x))
 = - \sin(x))
 = \sin(x))
 = \cos(x))
 = - \sin(x))
 = \cos(x))
 \, = \, \frac{e^{i \theta} + e^{- i \theta}}{2})
 \, = \, \frac{e^{i \theta} - e^{- i \theta}}{2i})
 = cos(a) \times cos(b) - sin(a) \times sin(b))
 = sin(a) \times cos(b) + sin(b) \times cos(a))
 = cos(a) \times cos(b) + sin(a) \times sin(b))
 = sin(a) \times cos(b) - sin(b) \times cos(a))
 = cos(a)^2 - sin(a)^2)
 = 2cos(a)^2 - 1)
 = 1 - 2sin(a)^2)
 = 2sin(a) \times cos(a))
^2 = \frac{1 + cos(2a)}{2})
^2 = \frac{1 - cos(2a)}{2})
![cos(a) cos(b) = frac{1}{2} [cos(a+b) + cos(a-b)] cos(a) cos(b) = \frac{1}{2} [cos(a+b) + cos(a-b)]](cgi-bin/latex.cgi?cos(a) cos(b) = \frac{1}{2} [cos(a+b) + cos(a-b)])
![sin(a) sin(b) = frac{1}{2} [- cos(a+b) + cos(a-b)] sin(a) sin(b) = \frac{1}{2} [- cos(a+b) + cos(a-b)]](cgi-bin/latex.cgi?sin(a) sin(b) = \frac{1}{2} [- cos(a+b) + cos(a-b)])
![sin(a) cos(b) = frac{1}{2} [sin(a+b) + sin(a-b)] sin(a) cos(b) = \frac{1}{2} [sin(a+b) + sin(a-b)]](cgi-bin/latex.cgi?sin(a) cos(b) = \frac{1}{2} [sin(a+b) + sin(a-b)])
) en fonction de
en fonction de ) :
:
... Un peu long et pas adapté dès qu'on veut faire












 est une inégalité vraie mais ce n'est pas la division euclidienne de 21 par 5. (car 6>5)
est une inégalité vraie mais ce n'est pas la division euclidienne de 21 par 5. (car 6>5) sont : 0, 1, 2, ..., b-1, ...
sont : 0, 1, 2, ..., b-1, ...
