Vous êtes ici : Accueil > Concours > Grandes écoles >CCP PSI 2006 - Exercice d'Oral

Concours -Grandes écoles

CCP PSI 2006 - Exercice d'Oral

  • Auteur :DarKnight
  • Créé le :01/06/2008
  • Modifié le :10/04/2013

Enoncé

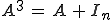
Montrer que A \in M_{n}(\mathbb R) telle que A^{3}\,=\,A\,+\,I_{n} est diagonalisable dans M_{n}(\mathbb C).
En déduire que \det A \,> \,0


Éléments de réponse

Se rappeler des conditions de diagonalisabilité (^^) d'une matrice.


Réponse

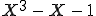
X^{3}\,-\,X\,-\,1 est un polynôme annulateur non nul. On peut l'écrire sous une forme scindée simple dans \mathbb C [X]. A possède donc un polynôme annulateur scindé simple.
Elle est diagonalisable dans M_{n}(\mathbb C).

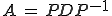
On peut donc l'écrire : A\,=\, PDP^{-1} où D est diagonale, et ses coefficients diagonaux sont complexes.
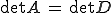
Le déterminant est invariant par changement de base, donc \det A \,=\, \det D.