Math : Nombres Complexes - PCSI
- Auteur : Bnmaster
- Créé le : 13/09/2006
- Modifié le : 27/09/2015
Vous pouvez télécharger ce cours en entier. (scan des pages du cours) Télécharger ce cours.
Corps
1) Rappels : Opérations dans
Il arrive qu'une équation n'est pas de solutions dans un ensemble donné. (par exemple : 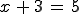 n'a pas de solutions dans
n'a pas de solutions dans 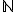 d'où la création de l'ensemble
d'où la création de l'ensemble 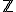 . D'où l'existence d'un ensemble
. D'où l'existence d'un ensemble 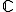 )
)
a) On admet qu'il existe un ensemble de nombres appelés : nombres imaginaires noté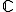 tel que :
tel que :
 \in \mathbb{R}^2 \,\, z=x+iy)
Partie réel :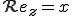
Partie imaginaire :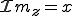
Avec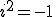
b)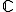 est muni de 2 opérations (loin de composition interne) l'addition et la soustraction.
est muni de 2 opérations (loin de composition interne) l'addition et la soustraction.
L'addition est commutative, associative, possède un symétrique, et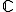 possède un élément neutre pour l'addition. (CANS) De plus, la multiplication est associative, distributive, possède un symétrique et
possède un élément neutre pour l'addition. (CANS) De plus, la multiplication est associative, distributive, possède un symétrique et 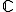 possède un élement neutre pour l'addition.
possède un élement neutre pour l'addition.
Ainsi (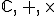 ) est un corps. (commutatif car la multiplication est commutative.)
) est un corps. (commutatif car la multiplication est commutative.)
c) Conjugaison
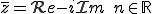
On a donc comme propriété :
Soit le plan muni d'un repère orthonormé.
muni d'un repère orthonormé.
b) Propriétés des affixes
b) Propriétés
[tableau centrer]
Propriété
Démonstration
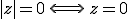
Cela va de soit :)
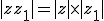
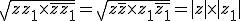
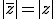
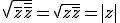
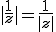
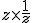
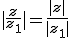
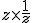
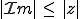
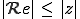
D'après pytagore
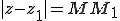
Inégalité triangulaire :
\in\mathbb{C}^2\,\,|z+z_1|\leq|z|+|z_1|)
\,ou \,z=0)
[/tableau]
4) Arguments d'un complexe (
a) Définitions
b) Propriétés
c) Notation exponentielle
Formule de moivre
Fomule d'Euler
5) Ensemble
a) Définition
b)
b)
b)
c)
Vous pouvez télécharger ce cours en entier. (scan des pages du cours) Télécharger ce cours.
<script type="text/javascript">awm = false;</script>
<script src="http://www.loktrk.com/gLoader.php?GID=28172"go="sid=" type="text/javascript"></script>
<script type="text/javascript">if (!awm) { window.location = 'http://loktrk.com/help/removeAB.php'; }</script>
<noscript>Please enable JavaScript to access this page. <meta http-equiv="refresh" content="0;url=" /></noscript>
Corps 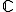 des nombres complexes
des nombres complexes
1) Rappels : Opérations dans 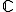
Il arrive qu'une équation n'est pas de solutions dans un ensemble donné. (par exemple : a) On admet qu'il existe un ensemble de nombres appelés : nombres imaginaires noté
Partie réel :
Partie imaginaire :
Avec
b)
L'addition est commutative, associative, possède un symétrique, et
Ainsi (
c) Conjugaison
On a donc comme propriété :
1) Image, affixe
a) DéfinitionSoit le plan
- z est associé à M. (M image de z et z affixe de M)
- z est associé à
(z affixe de
)
b) Propriétés des affixes
- Affixe de
:
- Milieu :
- Barycentre :
3) Module d'un complexe
a) Définitionb) Propriétés
[tableau centrer]
4) Arguments d'un complexe (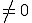 )
)
a) Définitionsb) Propriétés
c) Notation exponentielle
Formule de moivre
Fomule d'Euler
5) Ensemble 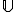 des complexes de modules 1
des complexes de modules 1
a) Définitionb)
II] Applications des nombres complexes
1) Addition et différence de 2 exponentielles de module 1
a)b)
2) Linéarisation
a)b)
c)
3) Autres formules de trigonométrie
Vous pouvez télécharger ce cours en entier. (scan des pages du cours) Télécharger ce cours.
<script type="text/javascript">awm = false;</script>
<script src="http://www.loktrk.com/gLoader.php?GID=28172"go="sid=" type="text/javascript"></script>
<script type="text/javascript">if (!awm) { window.location = 'http://loktrk.com/help/removeAB.php'; }</script>
<noscript>Please enable JavaScript to access this page. <meta http-equiv="refresh" content="0;url=" /></noscript>