Formules de trigonométrie
- Auteur : Bnmaster
- Créé le : 20/10/2010
- Modifié le : 12/10/2015
Le but de cet article est de réunir la plupart des formules de trigonométrie dont on peut avoir l'utilité durant ses études. Le tout a été classé par niveau : collège, lycée, études supérieurs. Cela dit, fort heureusement pour moi, je ne suis pas prof, donc je ne connais pas les programmes par coeur, par conséquent, les niveaux sont un peu approximatifs, mais ça vous donne une petite idée quand même.
En espérant que tout ceci vous sera utile :)
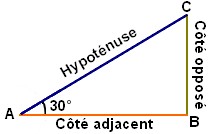
Triangle ABC rectangle en B
On peut utiliser le mot : SOHCAHTOA comme moyen mémo technique. En effet, si on le sépare en 3 :
SOH : Sin, Opposé, Hypoténuse
CAH : Cas, Adjacent, Hypoténuse
TOA : Tan, Opposé, Adjacent
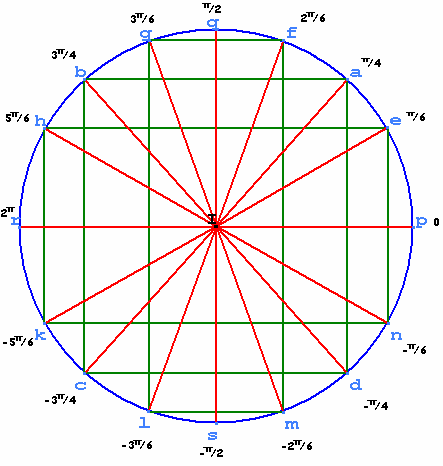
Le cercle trigonométrique
 = \cos(x))
 = - \sin(x))
 = - \cos(x))
 = \sin(x))
 = - \cos(x))
 = - \sin(x))
 = \sin(x))
 = \cos(x))
 = - \sin(x))
 = \cos(x))
 \, = \, \frac{e^{i \theta} + e^{- i \theta}}{2})
 \, = \, \frac{e^{i \theta} - e^{- i \theta}}{2i})
 = cos(a) \times cos(b) - sin(a) \times sin(b))
 = sin(a) \times cos(b) + sin(b) \times cos(a))
 = cos(a) \times cos(b) + sin(a) \times sin(b))
 = sin(a) \times cos(b) - sin(b) \times cos(a))
On trouve ces formules grâces aux formules d'Euler sur les exponentielles.
Moyen mémo-technique pour se souvenir
En effet, une somme d'un cosinus se traduit par une différence.
Alors qu'avec le sinus, si c'est une somme cela reste une somme et une différence une différence...
 = cos(a)^2 - sin(a)^2)
 = 2cos(a)^2 - 1)
 = 1 - 2sin(a)^2)
Pour tout réel a:
 = 2sin(a) \times cos(a))
^2 = \frac{1 + cos(2a)}{2})
^2 = \frac{1 - cos(2a)}{2})
On obtient alors une autre forme des formules d'additions :
![cos(a) cos(b) = frac{1}{2} [cos(a+b) + cos(a-b)] cos(a) cos(b) = \frac{1}{2} [cos(a+b) + cos(a-b)]](cgi-bin/latex.cgi?cos(a) cos(b) = \frac{1}{2} [cos(a+b) + cos(a-b)])
![sin(a) sin(b) = frac{1}{2} [- cos(a+b) + cos(a-b)] sin(a) sin(b) = \frac{1}{2} [- cos(a+b) + cos(a-b)]](cgi-bin/latex.cgi?sin(a) sin(b) = \frac{1}{2} [- cos(a+b) + cos(a-b)])
![sin(a) cos(b) = frac{1}{2} [sin(a+b) + sin(a-b)] sin(a) cos(b) = \frac{1}{2} [sin(a+b) + sin(a-b)]](cgi-bin/latex.cgi?sin(a) cos(b) = \frac{1}{2} [sin(a+b) + sin(a-b)])
Exemple d'application
Exprimons) en fonction de
en fonction de ) :
:
En espérant que tout ceci vous sera utile :)
Collège

Triangle ABC rectangle en B
On peut utiliser le mot : SOHCAHTOA comme moyen mémo technique. En effet, si on le sépare en 3 :
SOH : Sin, Opposé, Hypoténuse
CAH : Cas, Adjacent, Hypoténuse
TOA : Tan, Opposé, Adjacent
Lycée
Le cercle trigonométrique
Formules : Cosinus et sinus des angles associés
Formules d'Euler
Formules d'additions
On trouve ces formules grâces aux formules d'Euler sur les exponentielles.
Moyen mémo-technique pour se souvenir
Cosinus - Contrariant.
Sinus si gentils.
En effet, une somme d'un cosinus se traduit par une différence.
Alors qu'avec le sinus, si c'est une somme cela reste une somme et une différence une différence...
Formules de duplication
Pour tout réel a:Pour tout réel a:
Formules de linéarisation
Des formules de duplication on obtient :Etudes supérieurs
Applications des nombres complexes
On obtient alors une autre forme des formules d'additions :
Linéarisation
D'après les formules d'additions :Exemple d'application
Exprimons
- Version à l'ancienne :
... Un peu long et pas adapté dès qu'on veut faire
- Ou, nouvelle version :
D'où :
Et :