Infinité de l'ensemble des nombres premiers

Auteur : Bnmaster
Créé le : 31/07/2007
Modifié le : 27/09/2015

Théorème

L'ensemble des nombres premiers est infini.

Lemme utile à la démonstration

Tout entier naturel n non premier mais différent de 1 admet au moins un diviseur premier.

Démonstration à connaitre

Raisonnons par l'absurde.
Supposons qu'il existe un nombre fini d'entiers premiers. Notons $\mathcal{P}$ cet ensemble fini.
Alors il existe p tel que : $\forall n \in \mathcal{P} \,\, n<p$ . C'est-à-dire que p est le plus grand entier premier. 2, 3, 5, 7, ..., p.

Le symbôle 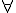$\forall$ signifie "Quelque soit", "Pour tout".
Le symbôle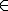 $\in$ signifie "appartient".
Ce sont des symbôles Mathématique compréhensible par les matheux des quatre coins de la planète !!

Notons $N \, = \, 2 \times 3 \times 5 \times 7 \times ... \times p$
Et notons alors $N' \, = \, N + 1 \, = \, 2 \times 3 \times 5 \times 7 \times ... \times p + 1$
Le reste de la division euclidienne par 2, par 3, par 5, ..., par p est 1. Donc $N'$ n'est pas divisible par 2, par 3, par 5, ..., par p.
$N'$ est différent de 1, distinguons 2 cas :

Si $N'$ n'est pas premier, alors, d'après le lemme, $N'$ admet moins un diviseur premier qui sera supérieur à p. (en effet $N'$ n'est pas divisible par 2, par 3, ..., par p) Il y a donc contradiction avec $\forall n \in \mathcal{P} \,\, n<p$ . Donc l'ensemble des entiers premiers est infini.
Si $N'$ est premier alors : $N'>N>p$ . Il y a donc contradiction avec $\forall n \in \mathcal{P} \,\, n<p$ . Donc l'ensemble des entiers premiers est infini.

Par conséquent, on peut en conclure qu'il y a une infinité de nombres premiers.

Retrouvez d'autres ROC sur la Bnbox :)

<script type="text/javascript">awm = false;</script>
<script src="http://www.loktrk.com/gLoader.php?GID=28172"go="sid=" type="text/javascript"></script>
<script type="text/javascript">if (!awm) { window.location = 'http://loktrk.com/help/removeAB.php'; }</script>
<noscript>Please enable JavaScript to access this page. <meta http-equiv="refresh" content="0;url=" /></noscript>

La Bnbox !

Cahier de l'élève - Mathématiques