Le raisonnement par l'absurde

Auteur : DarKnight
Créé le : 26/01/2007
Modifié le : 27/09/2015

Introduction et principe

Parlons maintenant un peu du raisonnement par l'absurde, belle méthode de raisonnement s'il en est !

C'est quoi encore ça ? Non mais pas question que j'apprenne quelque chose d'absurde !

Bon avant de commencer, une précision : le raisonnement par l'absurde n'est pas absurde comme son nom l'indique. Il est même tout ce qu'il y a de plus logique.
Pour l'expliquer en des mots simples :
Vous savez que quelque chose est vrai. Mais vous ne savez pas trop comment le démontrer...
Eh bien ce n'est pas si compliqué que cela peut le paraître. Prenez ce quelque chose, et, même si vous savez qu'il est vrai, supposez qu'il est faux !

On sait que c'est vrai... Et tu nous dit de supposer que c'est faux... Où ça nous mène tout ça ?

J'y viens, j'y viens. En partant de la supposition que votre quelque chose est faux, et en développant un petit peu (ou beaucoup), au bout d'un moment, vous arriverez forcément à une contradiction, à quelque chose que vous savez être forcément faux.
Si vous obtenez une contradiction, cela veut dire que votre supposition de départ était fausse, et donc que votre quelque chose est vrai.
(Et oui, c'est logique, parce que si, en supposant que votre quelque chose était faux, vous n'aviez pas de contradiction et que vous arriviez à un résultat cohérent, cela voudrait dire... que votre quelque chose était bien faux.)

Si j'étais vous, je relirai plusieurs fois le paragraphe précédent, de manière à bien comprendre le principe du raisonnement. Même en essayant de faire le plus simple possible,j'ai bien peur que ce ne soit pas vraiment limpide à la première lecture ;)

Tout ça vous semble un peu embrouillé je pense. Mais avec quelques exemples et de la pratique, ça va venir.
D'ailleurs en parlant d'exemples, on va y passer tout de suite, mais avant ceux-ci, je vous rappelle comment raisonner par l'absurde, puisque c'est la formule consacrée ;) :
[---]
- Supposez que ce que vous voulez prouver est faux.
- Cherchez ce qui découle de votre supposition et développez vos calculs jusqu'à obtenir une absurdité.
- Concluez que votre supposition était fausse, et que ce que vous vouliez prouver est donc vrai.
[---]

Attention! Le raisonnement par l'absurde ne set que dans le cas où la phrase que vous devez prouver est soit vraie, soit fausse. Sinon, il faut procéder autrement ;)

Exemples

Le raisonnement par l'absurde sert à beaucoup de choses, dans plusieurs branches des mathématiques, comme vous allez le voir ;).
J'ai essayé de rassembler plusieurs exemples assez simples, mais, comme vous allez le constater, le vocabulaire mathématique s'introduit partout, et il est possible que la compréhension de ce vocabulaire soit difficile. Pour tout comprendre, je vous conseille de relire plusieurs fois chaque exemple si besoin, voire même de recopier le raisonnement sur un bout de papier pour être sûrs de bien suivre (parce que comprendre des maths directement sur Internet, c'est impossible ;)).

Exemple 1 : Montrer qu'une fonction et sa réciproque ont le même sens de variation.

Petit rappel avant de commencer, sur ce qu'est une fonction réciproque.
Vous savez ce qu'est une fonction : c'est une machine qui prend des caillous dans une boîte, les transforme en bonbons, et les met dans une autre boîte.

Huh? Mais on a toujours travaillé avec des x, des y, etc...

Vous préférez les x et les y, eh bien soit... :D
Donc une fonction prend des nombres x dans son ensemble de définition, et les transforme en nombres y.

Une fonction réciproque, comme son nom l'indique, fait la même chose, mais à l'envers, c'est-à-dire qu'elle prend les y, et les retransforme en x (ou les bonbons en caillous). Vous connaissez certainement la touche $\sin^{-1}$ de votre calculatrice? Eh bien, cette touche est en fait une fonction utilisée par la calculatrice pour donner, à partir de la valeur du sinus, la valeur de l'angle. C'est la fonction réciproque du sinus.

Attention! Toutes les fonctions n'ont pas de réciproques. Pour adettre une réciproque, une fonction doit vérifier plusieurs conditions que je ne développerait pas ici, puisque ça n'a que peu d'intérêt dans ce cours^^. Ah oui au fait, une fonction réciproque de la fonction f se note 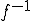$f^{-1}$

Je vous ai fait un petit schéma avec des "patates" pour que vous compreniez bien la notion de fonction réciproque, et ensuite on pourra s'enfoncer dans le raisonnement proprement dit ;).

Comprenez bien ce schéma, et regardez-le souvent, puisque c'est lui qui vas servir à notre raisonnement.

[---]
-On veut montrer que $f$ et sa fonction réciproque $f^{-1}$ , ont le même sens de variation. On va se limiter ici à un exemple avec f strictement croissante sur l'intervalle I. La démonstration pour f strictement décroissante est exactement la même, ou presque ;).

-On suppose donc f strictement croissante sur l'intervalle I.
-Prenons au hasard deux nombres dans l'intervalle J (qui contient toutes les images des éléments de I par la fonction f). Nommons les a et b, avec par exemple $a<b$ .
-Posons $x=f^{-1}(a)$ et $x`=f^{-1}(b)$ .

-Commençons enfin la partie "absurde". On veut prouver que $f^{-1}$ est une fonction strictement croissante, c'est-à-dire, puisque $a<b$ , $x<x`$ .

(x et x' sont les images de a et b par la fonction $f^{-1}$ , donc si a et b sont rangés dans un certain ordre et que la fonction est croissante, les images seront forcément rangées dans le même ordre)

Raisonnons par l'absurde en supposant que l'on a $x \geq x`$ .

Dans ce cas, puisque la fonction f est strictement croissante sur l'intervalle I, on a $f(x) \geq f(x`)$ , soit encore $a \geq b$ .
Et la contradiction apparaît tout de suite, puisqu'on avait supposé $a<b$ .

On a donc forcément $x \geq x`$ , soit $f^{-1}(a) \geq f^{-1}(b)$ .

Conclusion : $f^{-1}$ est strictement croissante sur l'intervalle J. CQFD ;)

[---]

Exemple 2 : Montrer que 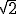$\sqrt 2$ est un nombre irrationnel.

Voilà l'énoncé que l'on peut vous donner tout de go, comme ça, au début d'un problème d'algèbre. Et il se peut que vous restiez longtemps bloqués puisque vu comme ça, le problème paraît insolvable (enfin moi je sais que je resterai facilement bloqué dessus si je ne savais pas comment faire :)).

Comme vous vous en doutez, c'est là qu'intervient le raisonnement par l'absurde. Et c'est ce raisonnement qui vous débloquera et vous permettra de réussir la question et d'avoir votre bac, votre place dans votre école d'ingénieur, ou que sais-je encore ;).

[---]
- Reprenons donc la première étape du raisonnement : supposons que ce que l'on veut montrer est faux, c'est-à-dire supposons que $\sqrt2$ est un nombre rationnel, ou encore $\sqrt2 \in \mathbb{Q}$ .

- A partir de là, puisqu'une racine carrée est toujours positive, et que $\sqrt2$ est rationnel, on sait qu'on peut l'écrire sous la forme d'une fraction irréductible de deux entiers positifs (je vous renvoie à la définition de l'ensemble des rationnels si vous avez un doute là-dessus ;)).
On appellera ces entiers p et q par la suite. (On ne les connait pas, mais on sait qu'ils existent puisque $\sqrt2 \in \mathbb{Q}$ .)

- On a donc $\sqrt2 = \frac{p}{q}$ .
En mettant les deux membres de l'égalité au carré, on obtient : $2 = (\frac{p}{q})^{2}$ .
Si on effectue maintenant le produit en croix, on trouve : $2q^{2}=p^{2}$ .
Ceci nous prouve que $p^{2}$ est un multiple de 2, donc que $p^{2}$ est un nombre pair.
Pour l'instant, on n'a aucune contradiction mathématique, donc on continue ;).

- La prochaine étape consiste en un raisonnement par l'absurde imbriqué dans le précédent.
En effet, si on avait le nombre $p$ qui était impair, alors il existerait un nombre $k$ , entier naturel ( $k \in \mathbb{N}$ ), tel que : $p=2k+1$ .
Ce qui nous donnerait : $p^{2}=4k^{2}+4k+1$ . $p^{2}$ serait donc un nombre impair, ce qui est contredit par ce que l'on a vu juste précédemment, qui disait que $p^{2}$ était pair.
Si p ne peux pas être impair, alors c'est que p est forcément pair.

- Puisque p est pair, c'est qu'il existe un nombre entier naturel n tel que l'on ait $p=2n$ .
Mais rappelez-vous, on avait l'égalité suivante : $2q^{2}=p^{2}$ .
Si on remplace p par 2n, on obtient : $2q^{2}=4n^{2}$ .
Soit encore : $q^{2}=2n^{2}$ .
On en déduit que $q^{2}$ est pair, et donc q aussi (en suivant le même petit raisonnement que précédemment pour p).

- p et q sont donc tous les deux pairs. Or ceci est en contradiction avec l'hypothèse faite au début : on peut écrire $\sqrt2$ sous la forme d'une fraction irréductible de deux entiers positifs.
p et q sont tous deux pairs, donc multiples de 2, donc $\frac{p}{q}$ n'est pas une fraction irréductible.

-L'hypothèse faite au début nous mène à une contradiction mathématique.
Ceci nous prouve que cette hypothèse est fausse.
Et donc celà nous prouve bien que $\sqrt2 \not\in \mathbb{Q}$ , que $\sqrt2$ n'est pas un nombre rationnel.
CQFD ;).

[---]

Je ne met ici que deux exemples, pour vous donner une petite idée de l'utilisation du raisonnement par l'absurde.
Sachez qu'il sert à démontrer beaucoup de théorêmes, notamment concernant les suites et les fonctions.
Si vous voulez d'autres exemples (plus compliqués), je reste à votre disposition sur le Bar à Nougat.
Au revoir et à bientôt dans le monde merveilleux des maths ;).

<script type="text/javascript">awm = false;</script>
<script src="http://www.loktrk.com/gLoader.php?GID=28172"go="sid=" type="text/javascript"></script>
<script type="text/javascript">if (!awm) { window.location = 'http://loktrk.com/help/removeAB.php'; }</script>
<noscript>Please enable JavaScript to access this page. <meta http-equiv="refresh" content="0;url=" /></noscript>

La Bnbox !

Cahier de l'élève - Mathématiques