Equations différentielles [partie 1]
- Auteur : DarKnight
- Créé le : 27/11/2006
- Modifié le : 27/09/2015
Ah... Les équations différentielles... Un mot qui fait peur...
Quand on arrive en Terminale, et que les profs commencent à en parler, qu'on a des sueurs froides qui commencent à couler dans le dos...
Enfin, vous vous êtes peut-être déjà rendus compte que ce n'était pas si compliqué que ça...
Et même si vous trouvez toujours ça hors de portée, je vais essayer ici de rendre la chose accessible.
Il faut savoir tout d'abord que les cas abordés ici sont avant tout théoriques, et qu'en général, résoudre une équation différentielle est plus facile.
Il faut aussi savoir que la résolution de ces équations demande un certain nombre de notions mathématiques prérequises.
Pas d'affolement... Normalement, si vous êtes en train d'étudier les équations différentielles... Eh bien vous savez tout ce qu'il faut savoir : comment dériver et trouver les primitives d'une fonction, et également tout ce qui concerne les fonctions "traditionnelles" (facile à dire :P), c'est-à-dire les fonctions trigonométriques (sinus, cosinus, tangente), les fonctions exponentielle et logarithme népérien, et les fonctions polynômiales.
Vous vous sentez à peu près au point sur tout ça ? C'est bon ? Alors accrochez votre ceinture, on va y aller ;).
Une équation différentielle... Qu'est-ce que c'est au juste ?
Même en essayant de rester le plus simple possible, il faudra de toute manière employer un vocabulaire un peu mathématique... J'essaierai de le limiter, mais faire des maths sans maths, c'est pas évident :D.
Une équation différentielle est donc une équation (comme son nom l'indique), dont les solutions ne sont pas des nombres, comme dans les équations traditionnelles, mais des fonctions. Elle se présente sous la forme d'une égalité, faisant intervenir la fonction cherchée (que j'appellerai f(t) par la suite dans mes exemples), et éventuellement ses dérivées (première, seconde, voire plus).
Exemples d'équations différentielles :
 = f`(t)+8)
ou bien
 + (\sin t) f`(t) + f(t) = 0 )
(On remarquera que la deuxième sera forcément plus difficile à résoudre que la première... D'ailleurs je n'en parlerai pas dans cette partie ;). Donc vous pouvez tout de suite l'enlever de votre esprit, c'était juste un exemple.)
Vocabulaire :
L'ordre d'une équation différentielle, correspond à la dérivée de la fonction recherchée que fait intervenir l'équation.
Par exemple, une équation où l'on aurait + ... ) serait une équation du troisième ordre, puisqu'elle contient la dérivée troisième de la fonction cherchée.
serait une équation du troisième ordre, puisqu'elle contient la dérivée troisième de la fonction cherchée.
Une équation du premier ordre fait seulement intervenir la première dérivée : ) .
.
Et ainsi de suite, je pense que vous avez compris... ;)
Les coefficients d'une équation différentielle sont les nombres ou les fonctions multipliant la fonction recherchée. Dans le cas de nombres, on parlera de coefficients constants, et s'il s'agit de fonctions, on parlera de coefficients variables.
Dans ces deux équations, les coefficients sont 1 et (8/9) pour la première ; et (sin t) et (cos t) pour la deuxième.
 + (8/9)f(t) = 0 )
f`(t) + (\cos t)f(t) = 5 )
Pendant qu'on a un exemple sous les yeux... Pourquoi ne pas parler du second membre. La première des équations est dite "sans second membre", et la deuxième en possède un.
Vous l'aurez compris, le second membre d'une équation est ce qui se trouve à droite de l'égalité ;).
Enfin, parlons de l'adjectif linéaire, souvent associé aux équations différentielles. Une équation différentielle linéaire est une équation différentielle qui ne fait pas apparaître de puissance de la fonction cherchée, ni de transformation particulière avec des sinus, des cosinus, ou des trucs horribles dans le même genre.
Un petit exemple pour bien fixer les choses : + (8/9)f(t) = 0 ) . Cette équation est linéaire.
. Cette équation est linéaire.
Par contre celle-ci ne l'est pas :^2 + (8/9)f(t) = 0 ) , puisqu'elle fait apparaître une puissance de la dérivée de la fonction qu'on cherche.
, puisqu'elle fait apparaître une puissance de la dérivée de la fonction qu'on cherche.
Celle-ci ne l'est pas non plus : + (8/9)f(t)^2 = 0 ) , pour la même raison.
, pour la même raison.
Et celle-ci encore moins :) + (\cos t)f(t) = 5 ) .
.
J'espère que vous êtes bien au point sur le vocabulaire, parce que maintenant je l'emploierai sans scrupules :P. Si vous avez le moindre problème, relisez une ou deux fois le tout, et ça devrait aller mieux ;). Et au pire, c'est en forgeant qu'on devient forgeron, et vous comprendrez mieux au fur et à mesure des exemples.
Pour la suite de ce cours sur les équations différentielles, je ne vous apprendrai qu'à résoudre les équations linéaires (cf plus haut pour ceux qui n'auraient pas compris de quoi il s'agit), du premier ordre.
Puis, dans une deuxième partie, on verra comment résoudre une équation différentielle du second ordre à coefficients constants... Mais c'est une autre histoire, plus longue que la première :P, donc on la racontera plus tard.
Les équations différentielles auxquelles on s'intéressera ici seront donc de la forme :
 + af(t) = b )
En prenant a et b deux fonctions continues sur un intervalle I quelconque (inclus dans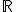 ou dans
ou dans 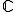 au choix).
au choix).
Ici, on prend a et b deux fonctions, pour faire une étude dans le cas le plus général. En pratique, on aura plus souvent affaire à des coefficients constants (dans les équations des circuits RC ou RL, ou dans des équations de mouvements en mécanique par exemple).
Fixez bien la forme de l'équation différentielle dans votre esprit, comme ça vous serez capable de la reconnaître au premier coup d'oeil quand vous en verrez une semblable. Et vous saurez tout de suite comment la résoudre (enfin j'espère :P).
Résoudre (on dit aussi "intégrer" dans le jargon des matheux ;) ) une équation différentielle, revient à trouver toutes les fonctions dérivables au moins sur I (intervalle où a et b sont continues je vous le rappelle), et qui vérifient la condition donnée par l'équation.
En général, on trouvera une infinité de fonctions qui correspondent à nos attentes, et dans les cas pratiques, on ne cherche qu'une seule de ces fonctions (par exemple pour savoir comment évolue la tension dans un circuit électrique). Dans ces cas-là, il y aura encore une petite opération à effectuer pour trouver LA seule et unique fonction que l'on veut. Mais j'en reparlerai tout à la fin de cette partie.
Commençons donc la partie difficile, à proprement parler, de ce cours.
Quand je parlais de partie "difficile", j'aurai plutôt dû dire la partie la plus "mathématique", puisque la manière de résoudre une équation différentielle est assez simple et répétitive. Par contre, elle demande de la rigueur.
Ce qui suit est la base de la résolution. C'est quelque chose de capital qu'il faut absolument retenir. Cela sert pour toutes les équations dont je parlerai (que ce soit dans la partie 1 ou dans la partie 2 de ce cours).
Rappelons tout d'abord le type d'équations différentielles étudiées ici :
 + af(t) = b ) (n'oubliez pas qu'ici on considère que a et b sont deux fonctions.)
(n'oubliez pas qu'ici on considère que a et b sont deux fonctions.)
Appelons (L) cette équation.
La méthode (qui a été étudiée par des dizaines de mathématiciens, et qui fonctionne assez bien :P) dit que pour résoudre cette équation différentielle, il faut :
[---]
1)Trouver l'ensemble des solutions de l'équation homogène associée à l'équation (L).
2)Trouver une fonction particulière qui serait solution de l'équation (L).
[---]
Eh bien j'ai préféré ne pas en parler avant pour vous faire la surprise ;). Mais vous allez voir ce n'est pas compliqué, c'est encore un problème de vocabulaire essentiellement.
Une équation homogène, est une équation différentielle à laquelle on a enlevé son second membre.
Dans le cas qui nous intéresse, l'équation homogène associée à l'équation (L) que l'on cherche à résoudre serait l'équation différentielle suivante : + af(t) = 0 ) .
.
Vous pouvez vérifier qu'on lui a bien retiré son second membre (on n'a plus la fonction b mais bien 0 à droite du signe "="). Pour plus de commodité, j'appellerai cette équation (H) par la suite (H comme Homogène :P).
On récapitule les équations que l'on a avant de continuer :
-L'équation que l'on veut résoudre : (L) : + af(t) = b ) .
.
-Son équation homogène associée : (H) : + af(t) = 0 ) .
.
Maintenant que les choses sont bien au clair, commençons notre résolution, c'est-à-dire cherchons toutes les fonctions qui sont solutions de l'équation différentielle (H).
Résolution de l'équation homogène
Là, vous vous dîtes sûrement que le problème reste entier... Puisque vous ne savez pas résoudre des équations qui font intervenir des fonctions.
Et pourtant... :)
Un théorème dit que pour trouver l'ensemble des solutions de (H), il suffit de trouver une solution particulière de (H), c'est-à-dire une fonction, telle que cette fonction (et sa dérivée), vérifie + af(t) = 0 ) , et telle qu'elle ne s'annule jamais sur l'intervalle I où l'on travaille.(C'est super important, puisque c'est ce qui nous assure qu'on ne divise pas par 0 quand on résout).
, et telle qu'elle ne s'annule jamais sur l'intervalle I où l'on travaille.(C'est super important, puisque c'est ce qui nous assure qu'on ne divise pas par 0 quand on résout).
Toutes les autres solutions de (H) seront tout simplement des multiples de cette solution particulière.
En d'autres termes, si on a trouvé une fonction g qui fonctionnerait pour (H), et qui ne s'annule jamais sur I, on peut dire que toutes les solutions de (H) sont de la forme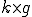 , avec k une constante quelconque appartenant à
, avec k une constante quelconque appartenant à 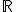 ou à
ou à 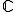 .
.
Ce théorème se démontre bien entendu, et assez simplement d'ailleurs, mais je ne compte pas vous donner la démonstration, puisque ce n'est pas vraiment ce qui vous intéresse ici :P. (Par contre si vous voulez vraiment connaître cette démonstration, rendez-vous sur le Bar à Nougat où je me ferai un plaisir de vous expliquer ;)).
Eh bien puisque vous vous impatientez, voici comment résoudre l'équation (H).
N'oublions pas avant de commencer que a est une fonction continue sur un intervalle I quelconque.
D'après le théorème cité plus haut, si on a une solution particulière de (H) qui ne s'annule jamais sur I, alors l'ensemble des solutions sont des multiples de cette solution particulière. (On évitera de choisir la fonction nulle comme solution particulière, parce que ca sera un peu embêtant de diviser par 0 un peu plus bas ;)).
(Attention, ce qui suit est une rédaction classique, ce qui veut dire que quand vous devez résoudre une équation différentielle, vous devez exactement écrire la même chose ;) ).
[---]
On suppose avoir une fonction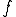 solution de (H), telle que
solution de (H), telle que 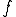 ne s'annule pas sur l'intervalle I, et soit différente de la fonction nulle.
ne s'annule pas sur l'intervalle I, et soit différente de la fonction nulle.
On a alors:
[---]
Et voilà on vient de finir de résoudre l'équation homogène (H). Toutes les solutions de cette équation sont toutes les fonctions de la forme = \lambda \times e^{-A(t)} ) , où
, où 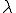 est une constante quelconque, et A(t) une primitive de la fonction a(t) qui se trouvait dans l'équation de départ.
est une constante quelconque, et A(t) une primitive de la fonction a(t) qui se trouvait dans l'équation de départ.
Vous remarquerez que j'ai tout expliqué dans le détail, et que quand vous serez bien entraînés (peut-être l'êtes-vous déjà ;)), eh bien vous n'aurez plus besoin de toutes ces étapes, et vous pourrez en sauter quelques unes. Mais il vaut mieux toujours comprendre dans le détail ce qu'on fait, avant d'aller plus vite ;).
Ah oui attention, n'oubliez pas de rajouter à toutes vos solutions la fonction nulle. Ca serait un peu bête de l'oublier alors que c'était une solution évidente ^^.
Trouver une solution particulière...
Après avoir résolu l'équation homogène (H), il reste la moitié du travail à accomplir. Puisque selon notre guide de travail, il nous faut encore trouver une solution particulière de (L). (Vous vous rappelez bien sûr que c'est (L) que l'on cherche à résoudre initialement :P... Non ? Bon je vous rappelle son expression: + a(t) \times f(t) = b(t) ) .)
.)
Cette partie du travail est parfois plus simple que la résolution de l'équation homogène, et parfois beaucoup plus complexe.
Tout dépendra en fait de la forme que prennent les fonctions b(t) et a(t).
Si a(t) est une constante, et que b(t) est une fonction relativement simple, la solution particulière recherchée sera en général de la même forme que la fonction b(t).
Je m'explique :
Si b(t) est une constante, on aura une solution particulière constante.
Si b(t) est un polynôme de degré n, on aura un polynôme de degré n qui sera solution particulière de (L).
Si c'est une exponentielle, de même.
Bon, tout ceci ne vous parle peut-être pas, donc, je vais essayer d'illustrer le tout du mieux possible, en traitant les cas les plus fréquents.
(Note : A la fin du cours sur les équations différentielles (donc quand on aura fini de traiter le second ordre ;)), je rajouterai une troisième partie concernant une méthode permettant à coup sûr de trouver une solution particulière, quelles que soient les formes de a(t) et b(t). Le problème est qu'elle est relativement compliquée à appliquer, et qu'on en a très peu souvent besoin.)
Enfin bref revenons à nos moutons. Essayez de bien suivre encore quelques minutes, et ca sera fini ^^.
Exemple 1 : Cas simple
Supposons qu'on ait une équation différentielle (L) de la forme : + a \times f(t) = b ) .
.
Ici a et b sont des constantes. Puisque le second membre (c'est-à-dire b) est une constante, on cherche une fonction particulière solution de l'équation sous la forme d'une constante.
Appelons g cette solution.
Puisque g est constante, on aura alors=0 )
En remplaçant la fonction f de l'équation différentielle par notre solution présumée g, on obtient :
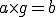
D'où, en passant le a de l'autre côté de l'égalité :
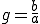
Et voilà on a trouvé la solution particulière de (L).
Il ne reste plus qu'à l'ajouter à notre solution générale de (H).
Dans ce cas-ci, la solution générale de (H) est de la forme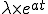 (je vous laisse le soin de refaire toute la démarche, ça vous entraînera ;)).
(je vous laisse le soin de refaire toute la démarche, ça vous entraînera ;)).
Donc les solutions de (L) sont toutes les fonctions de la forme : = \lambda \times e^{at} + \frac{b}{a} ) (où
(où 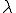 est une constante quelconque dans
est une constante quelconque dans 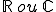
Exemple 2 : Cas plus compliqué
Supposons qu'on ait une équation différentielle de la forme : + 2 \times f(t) = \cos t ) .(Que l'on nommera (L).)
.(Que l'on nommera (L).)
Là on voit qu'on a une fonction cosinus qui sert de second membre à l'équation. Ici, on cherchera non-seulement du cosinus dans la solution particulière, mais également du sinus, puisqu'on sait parfaitement que la dérivée du cosinus est (-sinus), et donc il risque d'y avoir des sinus qui interviendront.
Dans le cas où on a des fonctions trigonométriques comme sinus ou cosinus, il faudra chercher une solution particulière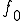 sous la forme :
sous la forme :  = C \times \cos t + D\times \sin t ) .
.
On suppose donc qu'on a une solution de cette forme, et il reste à déterminer les constantes C et D par un petit calcul, à l'aide de l'équation.
On peut maintenant trouver C et D. En prenant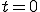 , on aura évidemment le terme en sinus qui s'annulera, et on aura alors :
, on aura évidemment le terme en sinus qui s'annulera, et on aura alors : 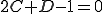 .
.
Ensuite il faut annuler le terme en cosinus, donc on prendra par exemple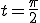 , et on aura :
, et on aura : 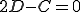
On a donc un petit système de deux équations à deux inconnues très facile à résoudre (je vous épargne les détails... peut-être dans un prochain cours ;)).
Au final on a :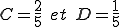
Notre solution particulière est donc : = \frac{2}{5}\times \cos t + \frac{1}{5} \times \sin t ) .
.
Et c'est gagné :D.
C'est vrai qu'on peut se poser la question. Puisqu'on a fini de résoudre l'équation différentielle...
Eh bien maintenant cela dépend de l'énoncé de votre exercice.
Si on vous demande toutes les solutions, pas besoin d'aller plus loin.
Mais le plus souvent, on vous demandera une seule solution, qui correspondra à un problème physique (puisque c'est en physique que les équations différentielles sont les plus utilisées).
Par exemple, si vous voulez connaître la loi d'évolution de la tension dans un circuit RC, il vous faut résoudre une équation différentielle du premier ordre, comme on vient de le faire. Mais puisque vous avez un circuit précis, il n'y a qu'une seule fonction qui définit l'évolution de la tension.
Il faudra donc la déterminer.
Et pour cela, il faut utiliser les fameuses... conditions initiales!!
Mais non mais non, qu'allez-vous vous imaginer ^^. C'est très simple.
Et puisque le cours s'éternise et qu'on est presque au bout, je vous montre juste un exemple, et vous pourrez le refaire à votre guise avec plein d'autres équations.
Sachez juste que pour une équation du premier ordre, vous n'avez besoin que d'une condition initiale, qui porte en général sur la fonction solution.
Pour une équation du second ordre, vous aurez besoin de deux conditions initiales, portant sur la fonction, et également sur sa dérivée.
Donc reprenons notre exemple précédent (le numéro 1).
On avait une équation différentielle linéaire du premier ordre à coefficients constants et à second membre constant de la forme : + a \times f(t) = b ) .
.
Et on avait trouvé que toutes les solutions étaient de la forme : = \lambda \times e^{at} + \frac{b}{a} ) (où
(où 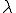 était une constante quelconque).
était une constante quelconque).
Supposons que cette équation différentielle est celle d'un système physique quelconque (électrique, mécanique, comme vous voulez^^).
On vous dit dans l'énoncé que vous devez trouver la loi d'évolution de la fonction f, en sachant qu'à l'instant initial (soit à t=0), vous avez=3 ) .
.
Alors, en utilisant la solution que l'on a, on peut écrire :
 = \lambda + \frac{b}{a} ) (Puisque
(Puisque 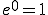 .)
.)
On a donc :
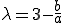 (En ordonnant simplement les termes de l'égalité.)
(En ordonnant simplement les termes de l'égalité.)
Et vous avez trouvé la seule valeur de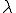 qui correspond à votre problème, et vous avez fini votre exercice :P.
qui correspond à votre problème, et vous avez fini votre exercice :P.
On refais la même chose quelque soit la forme de vos solutions, des fonctions a(t) et b(t). On se place toujours à t=0 et on utilise l'énoncé.
C'est encore un mathématicien mort qui l'a prouvé ;). Il s'appelait Cauchy, et il a montré qu'il n'existait qu'une unique solution de l'équation (L) qui correspondait à une condition initiale donnée. Je vous épargen encore une fois la démonstration, mais si elle vous intéresse, vous pouvez toujours aller la demander sur le Bar à Nougat ^^ (oui j'ai la flemme, et ça n'est pas vraiment fondamental ;)).
On vient d'apprendre à résoudre toutes sortes d'équations différentielles du premier ordre. C'est déjà pas mal ;).
Ce cours se voulait le plus général possible, donc je m'excuse par avance si les exemples ne sont pas assez concrets.
En mathématiques, on étudie principalement la méthode de résolution, comme ici. Donc si vous avez un exercice de maths sur les équations différentielles, vous devrez justifier vos calculs comme ici. Cependant, si c'est un exercice de physique, on part du principe que vous connaissez déjà la méthode, et donc vous n'avez pas besoin de tout justifier. Par exemple vous pourrez directement donner la forme de la solution de votre équation homogène, puisque vous aurez déjà résolu des tonnes et des tonnes d'équations du même type ;).
Je vais éviter de rajouter encore et encore des lignes à ce cours qui en fait déjà beaucoup, et je vais terminer par un petit résumé de ce qu'il faut faire pour résoudre une équation différentielle linéaire du premier ordre, histoire de bien mettre les choses au clair ;).
[---]
-Tout d'abord on cherche la forme générale des solutions de l'équation homogène associée.
-Puis on cherche une solution particulière de l'équation globale.
-Enfin, si on ne veut qu'une solution spécifique au problème posé, on utilise les conditions initiales pour la déterminer.
[---]
N'hésitez pas à vous inventer des équations et à les résoudre pour vous entraîner. La maîtrise vient avec la pratique ;).
Merci de votre attention, et à bientôt pour de nouvelles aventures dans le monde fabuleux des mathématiques^^.
<script type="text/javascript">awm = false;</script>
<script src="http://www.loktrk.com/gLoader.php?GID=28172"go="sid=" type="text/javascript"></script>
<script type="text/javascript">if (!awm) { window.location = 'http://loktrk.com/help/removeAB.php'; }</script>
<noscript>Please enable JavaScript to access this page. <meta http-equiv="refresh" content="0;url=" /></noscript>
Quand on arrive en Terminale, et que les profs commencent à en parler, qu'on a des sueurs froides qui commencent à couler dans le dos...
Enfin, vous vous êtes peut-être déjà rendus compte que ce n'était pas si compliqué que ça...
Et même si vous trouvez toujours ça hors de portée, je vais essayer ici de rendre la chose accessible.
Il faut savoir tout d'abord que les cas abordés ici sont avant tout théoriques, et qu'en général, résoudre une équation différentielle est plus facile.
Il faut aussi savoir que la résolution de ces équations demande un certain nombre de notions mathématiques prérequises.
Pas d'affolement... Normalement, si vous êtes en train d'étudier les équations différentielles... Eh bien vous savez tout ce qu'il faut savoir : comment dériver et trouver les primitives d'une fonction, et également tout ce qui concerne les fonctions "traditionnelles" (facile à dire :P), c'est-à-dire les fonctions trigonométriques (sinus, cosinus, tangente), les fonctions exponentielle et logarithme népérien, et les fonctions polynômiales.
Vous vous sentez à peu près au point sur tout ça ? C'est bon ? Alors accrochez votre ceinture, on va y aller ;).
Introduction
Une équation différentielle... Qu'est-ce que c'est au juste ?
Même en essayant de rester le plus simple possible, il faudra de toute manière employer un vocabulaire un peu mathématique... J'essaierai de le limiter, mais faire des maths sans maths, c'est pas évident :D.
Une équation différentielle est donc une équation (comme son nom l'indique), dont les solutions ne sont pas des nombres, comme dans les équations traditionnelles, mais des fonctions. Elle se présente sous la forme d'une égalité, faisant intervenir la fonction cherchée (que j'appellerai f(t) par la suite dans mes exemples), et éventuellement ses dérivées (première, seconde, voire plus).
Exemples d'équations différentielles :
ou bien
(On remarquera que la deuxième sera forcément plus difficile à résoudre que la première... D'ailleurs je n'en parlerai pas dans cette partie ;). Donc vous pouvez tout de suite l'enlever de votre esprit, c'était juste un exemple.)
Vocabulaire :
L'ordre d'une équation différentielle, correspond à la dérivée de la fonction recherchée que fait intervenir l'équation.
Par exemple, une équation où l'on aurait
Une équation du premier ordre fait seulement intervenir la première dérivée :
Et ainsi de suite, je pense que vous avez compris... ;)
Les coefficients d'une équation différentielle sont les nombres ou les fonctions multipliant la fonction recherchée. Dans le cas de nombres, on parlera de coefficients constants, et s'il s'agit de fonctions, on parlera de coefficients variables.
Dans ces deux équations, les coefficients sont 1 et (8/9) pour la première ; et (sin t) et (cos t) pour la deuxième.
Pendant qu'on a un exemple sous les yeux... Pourquoi ne pas parler du second membre. La première des équations est dite "sans second membre", et la deuxième en possède un.
Vous l'aurez compris, le second membre d'une équation est ce qui se trouve à droite de l'égalité ;).
Enfin, parlons de l'adjectif linéaire, souvent associé aux équations différentielles. Une équation différentielle linéaire est une équation différentielle qui ne fait pas apparaître de puissance de la fonction cherchée, ni de transformation particulière avec des sinus, des cosinus, ou des trucs horribles dans le même genre.
Un petit exemple pour bien fixer les choses :
Par contre celle-ci ne l'est pas :
Celle-ci ne l'est pas non plus :
Et celle-ci encore moins :
J'espère que vous êtes bien au point sur le vocabulaire, parce que maintenant je l'emploierai sans scrupules :P. Si vous avez le moindre problème, relisez une ou deux fois le tout, et ça devrait aller mieux ;). Et au pire, c'est en forgeant qu'on devient forgeron, et vous comprendrez mieux au fur et à mesure des exemples.
Résolution : comment faire ? Méthode générale.
Equations étudiées
Pour la suite de ce cours sur les équations différentielles, je ne vous apprendrai qu'à résoudre les équations linéaires (cf plus haut pour ceux qui n'auraient pas compris de quoi il s'agit), du premier ordre.
Puis, dans une deuxième partie, on verra comment résoudre une équation différentielle du second ordre à coefficients constants... Mais c'est une autre histoire, plus longue que la première :P, donc on la racontera plus tard.
Les équations différentielles auxquelles on s'intéressera ici seront donc de la forme :
En prenant a et b deux fonctions continues sur un intervalle I quelconque (inclus dans
Ici, on prend a et b deux fonctions, pour faire une étude dans le cas le plus général. En pratique, on aura plus souvent affaire à des coefficients constants (dans les équations des circuits RC ou RL, ou dans des équations de mouvements en mécanique par exemple).
Fixez bien la forme de l'équation différentielle dans votre esprit, comme ça vous serez capable de la reconnaître au premier coup d'oeil quand vous en verrez une semblable. Et vous saurez tout de suite comment la résoudre (enfin j'espère :P).
Mais au fait... résoudre cette équation, comme tu dis, ça revient à faire quoi ?
Résoudre (on dit aussi "intégrer" dans le jargon des matheux ;) ) une équation différentielle, revient à trouver toutes les fonctions dérivables au moins sur I (intervalle où a et b sont continues je vous le rappelle), et qui vérifient la condition donnée par l'équation.
En général, on trouvera une infinité de fonctions qui correspondent à nos attentes, et dans les cas pratiques, on ne cherche qu'une seule de ces fonctions (par exemple pour savoir comment évolue la tension dans un circuit électrique). Dans ces cas-là, il y aura encore une petite opération à effectuer pour trouver LA seule et unique fonction que l'on veut. Mais j'en reparlerai tout à la fin de cette partie.
Commençons donc la partie difficile, à proprement parler, de ce cours.
Méthode de résolution
Quand je parlais de partie "difficile", j'aurai plutôt dû dire la partie la plus "mathématique", puisque la manière de résoudre une équation différentielle est assez simple et répétitive. Par contre, elle demande de la rigueur.
Ce qui suit est la base de la résolution. C'est quelque chose de capital qu'il faut absolument retenir. Cela sert pour toutes les équations dont je parlerai (que ce soit dans la partie 1 ou dans la partie 2 de ce cours).
Rappelons tout d'abord le type d'équations différentielles étudiées ici :
Appelons (L) cette équation.
La méthode (qui a été étudiée par des dizaines de mathématiciens, et qui fonctionne assez bien :P) dit que pour résoudre cette équation différentielle, il faut :
[---]
1)Trouver l'ensemble des solutions de l'équation homogène associée à l'équation (L).
2)Trouver une fonction particulière qui serait solution de l'équation (L).
[---]
Attends attends!! Qu'est-ce que c'est encore que ça ? Une équation homogène ? Mais de quoi tu nous parle ?
Eh bien j'ai préféré ne pas en parler avant pour vous faire la surprise ;). Mais vous allez voir ce n'est pas compliqué, c'est encore un problème de vocabulaire essentiellement.
Une équation homogène, est une équation différentielle à laquelle on a enlevé son second membre.
Dans le cas qui nous intéresse, l'équation homogène associée à l'équation (L) que l'on cherche à résoudre serait l'équation différentielle suivante :
Vous pouvez vérifier qu'on lui a bien retiré son second membre (on n'a plus la fonction b mais bien 0 à droite du signe "="). Pour plus de commodité, j'appellerai cette équation (H) par la suite (H comme Homogène :P).
On récapitule les équations que l'on a avant de continuer :
-L'équation que l'on veut résoudre : (L) :
-Son équation homogène associée : (H) :
Maintenant que les choses sont bien au clair, commençons notre résolution, c'est-à-dire cherchons toutes les fonctions qui sont solutions de l'équation différentielle (H).
Résolution de l'équation homogène
Là, vous vous dîtes sûrement que le problème reste entier... Puisque vous ne savez pas résoudre des équations qui font intervenir des fonctions.
Et pourtant... :)
Un théorème dit que pour trouver l'ensemble des solutions de (H), il suffit de trouver une solution particulière de (H), c'est-à-dire une fonction, telle que cette fonction (et sa dérivée), vérifie
Toutes les autres solutions de (H) seront tout simplement des multiples de cette solution particulière.
En d'autres termes, si on a trouvé une fonction g qui fonctionnerait pour (H), et qui ne s'annule jamais sur I, on peut dire que toutes les solutions de (H) sont de la forme
Ce théorème se démontre bien entendu, et assez simplement d'ailleurs, mais je ne compte pas vous donner la démonstration, puisque ce n'est pas vraiment ce qui vous intéresse ici :P. (Par contre si vous voulez vraiment connaître cette démonstration, rendez-vous sur le Bar à Nougat où je me ferai un plaisir de vous expliquer ;)).
Bon, tout ça c'est bien joli, mais ça n'aide pas à résoudre le problème...
Eh bien puisque vous vous impatientez, voici comment résoudre l'équation (H).
N'oublions pas avant de commencer que a est une fonction continue sur un intervalle I quelconque.
D'après le théorème cité plus haut, si on a une solution particulière de (H) qui ne s'annule jamais sur I, alors l'ensemble des solutions sont des multiples de cette solution particulière. (On évitera de choisir la fonction nulle comme solution particulière, parce que ca sera un peu embêtant de diviser par 0 un peu plus bas ;)).
(Attention, ce qui suit est une rédaction classique, ce qui veut dire que quand vous devez résoudre une équation différentielle, vous devez exactement écrire la même chose ;) ).
[---]
On suppose avoir une fonction
On a alors:
| (Le petit ~ sur le 0 signifie que f est différent de la fonction nulle.) | |||
| |
| (On divise par f(t), c'est pour cela qu'on a supposé f ne s'annulant jamais, et différente de la fonction nulle.) | |
| |
| (On passe la fonction a de l'autre côté de l'égalité.) | |
| |
| (On sait que la primitive de (u'/u) est ln (u). Et on nomme A(t) la primitive de a(t), en n'oubliant pas la constante d'intégration. Cette constante, qu'on ne connaît pas, peut également s'écrire sous la forme |
|
| |
| (On passe |
|
| |
| (Grâce aux propriétés basiques du logarithme népérien, on réunit les logarithmes pour n'en avoir plus qu'un seul.) | |
| |
| (On utilise l'exponentielle pour se débarrasser du logarithme, puisque ces deux fonctions sont réciproques.) | |
| |
| (On repasse |
[---]
Et voilà on vient de finir de résoudre l'équation homogène (H). Toutes les solutions de cette équation sont toutes les fonctions de la forme
Vous remarquerez que j'ai tout expliqué dans le détail, et que quand vous serez bien entraînés (peut-être l'êtes-vous déjà ;)), eh bien vous n'aurez plus besoin de toutes ces étapes, et vous pourrez en sauter quelques unes. Mais il vaut mieux toujours comprendre dans le détail ce qu'on fait, avant d'aller plus vite ;).
Ah oui attention, n'oubliez pas de rajouter à toutes vos solutions la fonction nulle. Ca serait un peu bête de l'oublier alors que c'était une solution évidente ^^.
Trouver une solution particulière...
Après avoir résolu l'équation homogène (H), il reste la moitié du travail à accomplir. Puisque selon notre guide de travail, il nous faut encore trouver une solution particulière de (L). (Vous vous rappelez bien sûr que c'est (L) que l'on cherche à résoudre initialement :P... Non ? Bon je vous rappelle son expression:
Cette partie du travail est parfois plus simple que la résolution de l'équation homogène, et parfois beaucoup plus complexe.
Tout dépendra en fait de la forme que prennent les fonctions b(t) et a(t).
Si a(t) est une constante, et que b(t) est une fonction relativement simple, la solution particulière recherchée sera en général de la même forme que la fonction b(t).
Je m'explique :
Si b(t) est une constante, on aura une solution particulière constante.
Si b(t) est un polynôme de degré n, on aura un polynôme de degré n qui sera solution particulière de (L).
Si c'est une exponentielle, de même.
Bon, tout ceci ne vous parle peut-être pas, donc, je vais essayer d'illustrer le tout du mieux possible, en traitant les cas les plus fréquents.
(Note : A la fin du cours sur les équations différentielles (donc quand on aura fini de traiter le second ordre ;)), je rajouterai une troisième partie concernant une méthode permettant à coup sûr de trouver une solution particulière, quelles que soient les formes de a(t) et b(t). Le problème est qu'elle est relativement compliquée à appliquer, et qu'on en a très peu souvent besoin.)
Enfin bref revenons à nos moutons. Essayez de bien suivre encore quelques minutes, et ca sera fini ^^.
Exemple 1 : Cas simple
Supposons qu'on ait une équation différentielle (L) de la forme :
Ici a et b sont des constantes. Puisque le second membre (c'est-à-dire b) est une constante, on cherche une fonction particulière solution de l'équation sous la forme d'une constante.
Appelons g cette solution.
Puisque g est constante, on aura alors
En remplaçant la fonction f de l'équation différentielle par notre solution présumée g, on obtient :
D'où, en passant le a de l'autre côté de l'égalité :
Et voilà on a trouvé la solution particulière de (L).
Il ne reste plus qu'à l'ajouter à notre solution générale de (H).
Dans ce cas-ci, la solution générale de (H) est de la forme
Donc les solutions de (L) sont toutes les fonctions de la forme :
Exemple 2 : Cas plus compliqué
Supposons qu'on ait une équation différentielle de la forme :
Là on voit qu'on a une fonction cosinus qui sert de second membre à l'équation. Ici, on cherchera non-seulement du cosinus dans la solution particulière, mais également du sinus, puisqu'on sait parfaitement que la dérivée du cosinus est (-sinus), et donc il risque d'y avoir des sinus qui interviendront.
Dans le cas où on a des fonctions trigonométriques comme sinus ou cosinus, il faudra chercher une solution particulière
On suppose donc qu'on a une solution de cette forme, et il reste à déterminer les constantes C et D par un petit calcul, à l'aide de l'équation.
| (On dérive notre solution supposée, et on l'écris dans l'équation.) | |||
| (On passe le cosinus du second membre dans le premier, et on factorise par sinus et cosinus.) |
On peut maintenant trouver C et D. En prenant
Ensuite il faut annuler le terme en cosinus, donc on prendra par exemple
On a donc un petit système de deux équations à deux inconnues très facile à résoudre (je vous épargne les détails... peut-être dans un prochain cours ;)).
Au final on a :
Notre solution particulière est donc :
Et c'est gagné :D.
Et maintenant que fait-on ?
C'est vrai qu'on peut se poser la question. Puisqu'on a fini de résoudre l'équation différentielle...
Eh bien maintenant cela dépend de l'énoncé de votre exercice.
Si on vous demande toutes les solutions, pas besoin d'aller plus loin.
Mais le plus souvent, on vous demandera une seule solution, qui correspondra à un problème physique (puisque c'est en physique que les équations différentielles sont les plus utilisées).
Par exemple, si vous voulez connaître la loi d'évolution de la tension dans un circuit RC, il vous faut résoudre une équation différentielle du premier ordre, comme on vient de le faire. Mais puisque vous avez un circuit précis, il n'y a qu'une seule fonction qui définit l'évolution de la tension.
Il faudra donc la déterminer.
Et pour cela, il faut utiliser les fameuses... conditions initiales!!
Encore des ennuis en perspectives...
Mais non mais non, qu'allez-vous vous imaginer ^^. C'est très simple.
Et puisque le cours s'éternise et qu'on est presque au bout, je vous montre juste un exemple, et vous pourrez le refaire à votre guise avec plein d'autres équations.
Sachez juste que pour une équation du premier ordre, vous n'avez besoin que d'une condition initiale, qui porte en général sur la fonction solution.
Pour une équation du second ordre, vous aurez besoin de deux conditions initiales, portant sur la fonction, et également sur sa dérivée.
Donc reprenons notre exemple précédent (le numéro 1).
On avait une équation différentielle linéaire du premier ordre à coefficients constants et à second membre constant de la forme :
Et on avait trouvé que toutes les solutions étaient de la forme :
Supposons que cette équation différentielle est celle d'un système physique quelconque (électrique, mécanique, comme vous voulez^^).
On vous dit dans l'énoncé que vous devez trouver la loi d'évolution de la fonction f, en sachant qu'à l'instant initial (soit à t=0), vous avez
Alors, en utilisant la solution que l'on a, on peut écrire :
On a donc :
Et vous avez trouvé la seule valeur de
On refais la même chose quelque soit la forme de vos solutions, des fonctions a(t) et b(t). On se place toujours à t=0 et on utilise l'énoncé.
Euh oui d'accord, mais qu'est-ce qui me dit qu'il n'y a qu'une seule des solutions qui correspond à cette condition initiale ?
C'est encore un mathématicien mort qui l'a prouvé ;). Il s'appelait Cauchy, et il a montré qu'il n'existait qu'une unique solution de l'équation (L) qui correspondait à une condition initiale donnée. Je vous épargen encore une fois la démonstration, mais si elle vous intéresse, vous pouvez toujours aller la demander sur le Bar à Nougat ^^ (oui j'ai la flemme, et ça n'est pas vraiment fondamental ;)).
Au final...
On vient d'apprendre à résoudre toutes sortes d'équations différentielles du premier ordre. C'est déjà pas mal ;).
Ce cours se voulait le plus général possible, donc je m'excuse par avance si les exemples ne sont pas assez concrets.
En mathématiques, on étudie principalement la méthode de résolution, comme ici. Donc si vous avez un exercice de maths sur les équations différentielles, vous devrez justifier vos calculs comme ici. Cependant, si c'est un exercice de physique, on part du principe que vous connaissez déjà la méthode, et donc vous n'avez pas besoin de tout justifier. Par exemple vous pourrez directement donner la forme de la solution de votre équation homogène, puisque vous aurez déjà résolu des tonnes et des tonnes d'équations du même type ;).
Je vais éviter de rajouter encore et encore des lignes à ce cours qui en fait déjà beaucoup, et je vais terminer par un petit résumé de ce qu'il faut faire pour résoudre une équation différentielle linéaire du premier ordre, histoire de bien mettre les choses au clair ;).
[---]
-Tout d'abord on cherche la forme générale des solutions de l'équation homogène associée.
-Puis on cherche une solution particulière de l'équation globale.
-Enfin, si on ne veut qu'une solution spécifique au problème posé, on utilise les conditions initiales pour la déterminer.
[---]
N'hésitez pas à vous inventer des équations et à les résoudre pour vous entraîner. La maîtrise vient avec la pratique ;).
Merci de votre attention, et à bientôt pour de nouvelles aventures dans le monde fabuleux des mathématiques^^.
<script type="text/javascript">awm = false;</script>
<script src="http://www.loktrk.com/gLoader.php?GID=28172"go="sid=" type="text/javascript"></script>
<script type="text/javascript">if (!awm) { window.location = 'http://loktrk.com/help/removeAB.php'; }</script>
<noscript>Please enable JavaScript to access this page. <meta http-equiv="refresh" content="0;url=" /></noscript>











 est une inégalité vraie mais ce n'est pas la division euclidienne de 21 par 5. (car 6>5)
est une inégalité vraie mais ce n'est pas la division euclidienne de 21 par 5. (car 6>5) sont : 0, 1, 2, ..., b-1, ...
sont : 0, 1, 2, ..., b-1, ...